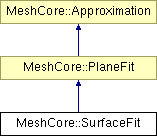
MeshCore::SurfaceFit Class Reference
Dies ist ein 2,5D-Ansatz, bei dem zunächst die Ausgleichsebene der Punktmenge (P_i = (x,y,z), i=1,. More...
#include <Approximation.h>
Public Member Functions | |
| float | Fit () |
| Fit a plane into the given points. | |
| bool | GetCurvatureInfo (float x, float y, float z, float &rfCurv0, float &rfcurv1) |
| bool | GetCurvatureInfo (float x, float y, float z, float &rfCurv0, float &rfCurv1, Base::Vector3f &rkDir0, Base::Vector3f &rkDir1, float &dDistance) |
| SurfaceFit () | |
| Construction. | |
| float | Value (float x, float y) const |
| virtual | ~SurfaceFit () |
| Destruction. | |
Protected Member Functions | |
| float | PolynomFit () |
Protected Attributes | |
| float | _fCoeff [10] |
| Ziel der Koeffizienten aus dem Fit. | |
Detailed Description
Dies ist ein 2,5D-Ansatz, bei dem zunächst die Ausgleichsebene der Punktmenge (P_i = (x,y,z), i=1,.
..,n) bestimmt wird. Danach wird eine Parametrisierung der Datenpunkte errechnet. Die Datenpunkte werden somit bzgl. des lokalen Systems der Ebene dargestellt (P_i = (u,v,w)). Durch diese transformierten Punkte wird nun eine quadratische Funktion w = f(u,v) = a*u^2 + b*v^2 + c*u*v + d*u + e*v + f berechnet. Dieser Ansatz wurde als Alternative für den 3D-Ansatz mit Quadriken entwickelt, da bei Quadriken in (vor allem) ebenen Bereichen recht seltsame Artefakte auftreten.
Definition at line 266 of file Approximation.h.
Constructor & Destructor Documentation
| SurfaceFit::SurfaceFit | ( | ) |
| virtual MeshCore::SurfaceFit::~SurfaceFit | ( | ) | [inline, virtual] |
Destruction.
Definition at line 276 of file Approximation.h.
Member Function Documentation
| float SurfaceFit::Fit | ( | ) | [virtual] |
Fit a plane into the given points.
We must have at least three non-collinear points to succeed. If the fit fails FLOAT_MAX is returned.
Reimplemented from MeshCore::PlaneFit.
Definition at line 518 of file Approximation.cpp.
References MeshCore::Approximation::_bIsFitted, MeshCore::Approximation::_fLastResult, MeshCore::Approximation::CountPoints(), FLOAT_MAX, and PolynomFit().
| bool SurfaceFit::GetCurvatureInfo | ( | float | x, | |
| float | y, | |||
| float | z, | |||
| float & | rfCurv0, | |||
| float & | rfcurv1 | |||
| ) |
Definition at line 550 of file Approximation.cpp.
References MeshCore::Approximation::_bIsFitted, _fCoeff, and MeshCore::FunctionContainer::CurvatureInfo().
| bool SurfaceFit::GetCurvatureInfo | ( | float | x, | |
| float | y, | |||
| float | z, | |||
| float & | rfCurv0, | |||
| float & | rfCurv1, | |||
| Base::Vector3f & | rkDir0, | |||
| Base::Vector3f & | rkDir1, | |||
| float & | dDistance | |||
| ) |
Definition at line 532 of file Approximation.cpp.
References MeshCore::Approximation::_bIsFitted, _fCoeff, MeshCore::Approximation::Convert(), MeshCore::FunctionContainer::CurvatureInfo(), MeshCore::FunctionContainer::GetGradient(), and Base::Vector3< _Precision >::Length().
| float SurfaceFit::PolynomFit | ( | ) | [protected] |
Definition at line 563 of file Approximation.cpp.
References _fCoeff, MeshCore::PlaneFit::_vBase, MeshCore::PlaneFit::_vDirU, MeshCore::PlaneFit::_vDirV, MeshCore::PlaneFit::_vDirW, MeshCore::Approximation::_vPoints, FemExample::b, MeshCore::PlaneFit::Fit(), FLOAT_MAX, boost::numeric::bindings::atlas::gesv(), Base::Vector3< _Precision >::TransformToCoordinateSystem(), Base::Vector3< _Precision >::x, Base::Vector3< _Precision >::y, and Base::Vector3< _Precision >::z.
Referenced by Fit().
| float SurfaceFit::Value | ( | float | x, | |
| float | y | |||
| ) | const |
Definition at line 673 of file Approximation.cpp.
References MeshCore::Approximation::_bIsFitted, _fCoeff, SketcherExample::f, and MeshCore::FunctionContainer::F().
Member Data Documentation
float MeshCore::SurfaceFit::_fCoeff[10] [protected] |
Ziel der Koeffizienten aus dem Fit.
Definition at line 286 of file Approximation.h.
Referenced by GetCurvatureInfo(), PolynomFit(), SurfaceFit(), and Value().
The documentation for this class was generated from the following files:
 1.6.1
1.6.1